Koordinat Sistemleri, Konum ve Hareket (Coordinate Systems, Position and Movement)

Mekanizmaları oluşturan makine elemanlarının bir eklem üzerinden birbirlerine göre hareketlenebildiklerini ifade etmiştik. Şimdi bu hareketin nasıl tanımlandığını görelim.

Konum (Position):  Bir noktanın yerinin referans kabul edilen bir başka noktaya göre tanımlanmasına o noktanın konumu denir.

Eğer bir noktanın konumu, tanım gereği uzayda birden fazla nokta olacak şekilde tanımlanabiliyorsa buna geometrik yer adı verilir. Bir başka deyişle geometrik yer; bir noktanın yer tanımını sağlayan bütün konumlardır.

Örneğin düzlemde sabit bir noktadan sabit uzaklıktaki bir noktadan bahsedersek sonsuz tane nokta buluruz. Bu tanımı sağlayan noktaların geometrik yeri bir çemberdir. Aynı şekilde uzayda sabit bir noktadan sabit uzaklıktaki noktaların geometrik yeri ise bir küre yüzeyidir. Çünkü çember ve küre yüzeyindeki sonsuz noktanın herhangi birisi verilen tanımı sağlamaktadır.

Oysa konumun yalnızca bir noktayı sağlıyor olması gerekir. Bu nedenle referans noktasına göre tanımlanmış koordinat sistemi üzerinden konum tanımlaması yaparız.

Koordinat Sistemleri (Coordinane Systems)

Koordinat sistemleri içinde bulunduğumuz evreni nasıl algıladığımızla ilgili olarak değişik biçimlerde tanımlanmaktadır. Bunlar; kartezyen koordinatlar ve kutupsal koordinat sistemleridir. Kutupsal koordinatlar küresel ve silindirik koordinat sistemleri olarak ayrıca ikiye ayrılır.

Kartezyen Koordinat Sistemi (Cartesian Coordinate System)

Çoğunlukla kullandığımız tek düzlemli uzayda, yani 2 boyutlu uzayda ise z büyüklüğü ihmal edilmekte veya sıfır kabul edilmektedir.

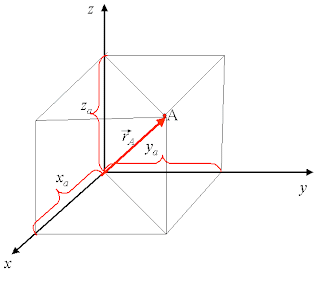
Bu sistemde uzaydaki bir noktanın yeri P(x, y, z) parametreleriyle, düzlemde ise P(x, y) ile verilir. 

Kutupsal Koordinat Sistemleri (Polar Coordainate Systems)

Burada P noktasının konumu O referans noktasına göre verilirken P nin O dan r kadar uzakta olduğu ile, O dan sağa doğru çizilen yatay referans doğrultusu ile OP doğru parçasının saat yönünün tersine doğru yaptığı açı bilgisi kullanılmaktadır.

Yani P noktasının O ya göre konumu P( r, q ) ile verilmektedir.

Eğer kutuplu polar koordinat sistemine 3. Boyutu eklemek istersek önümüzde iki seçenek vardır. Bunlardan ilki; noktanın zemin düzleminden yüksekliğini (h) vermektir. Bu gösterilime silindirik koordinat sistemi denir. Bu durumda noktanın koordinatları P( r, q, h) olarak gösterilir.

İkincisi; yarıçap doğrusunu içine alan ve zemin düzlemine dik olan yeni bir düzleminde yarıçap doğrusu ile yaptığı açıdır (f). Noktanın koordinatları ise P( r, q, f) olur.